使用 PyTorch 进行线性回归模型训练实战

2025年9月13日

使用 PyTorch 进行线性回归模型训练实战

本文结合个人实验的Jupyter Notebook示例，从零开始使用PyTorch完成一个线形回归模型的构建、训练与理解。内容面向初学者，同时也帮助你建立对 PyTorch 自动求导与训练流程的正确认知。

一、线性回归问题回顾

线性回归是最基础的监督学习模型，其数学形式为：

\hat{y} = w x + b

其中：

$x$ ：输入特征
$w$ ：权重（weight）
$b$ ：偏置（bias）
$\hat{y}$ ：预测值

模型训练的目标是通过数据学习合适的 $w$ , $b$ ，使预测值 $\hat{y}$ 尽可能接近真实值 $y$ 。

二、PyTorch 基础：Tensor 与自动求导

什么是Tensor

在Jupyter Notebook的环境里，先安装好torch，然后新建一个tensor示例，如下：

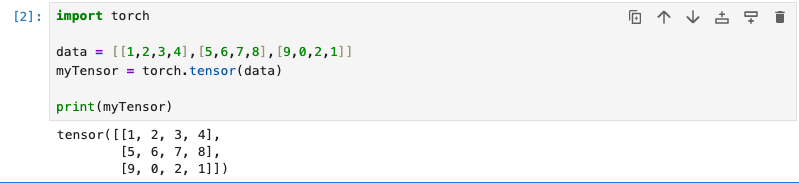
crttensorsim

这个是一个最简单的Tensor，它不带梯度，由一个矩阵数组构造而来。Tensor有几个重要属性，包括：shape，dtype，以及device。

shape: 它的含义就是矩阵的形状，几行几列。
dtype: 它表示元素的数据类型。
device: 它表示的是使用的设备类型，一般为cpu，或者cuda。

device为cuda的是启用Nvdia的CUDA机制，通过GPU进行计算，可以显著提高Tensor的计算效率。

示例如下图：

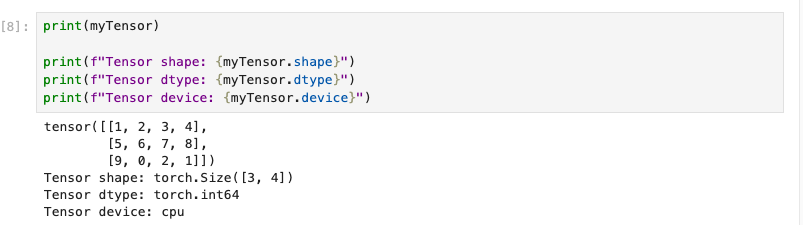
tensorshape

由此可见，Tensor是一种矩阵的数据封装器，那么再来探索一下这个矩阵封装器的其他特性。

Tensor的自动求导

我们探索了 Tensor 的创建与属性，下面是一个做ML/LLM都会用到的参数requires_grad，这是创建自动求导Tensor的核心数据结构:

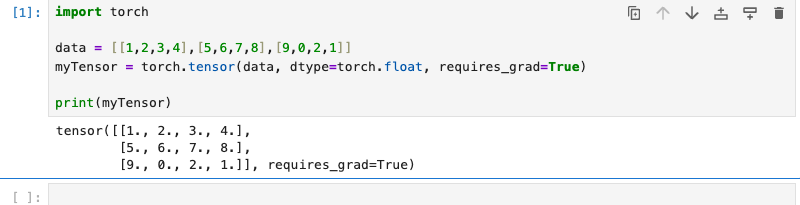
tensorautograd

requires_grad 表示对Tensor进行计算时，可以跟踪它的计算过程，将来可以对它求导（梯度计算）。

示例如下，首先使用Tensor进行系列计算：

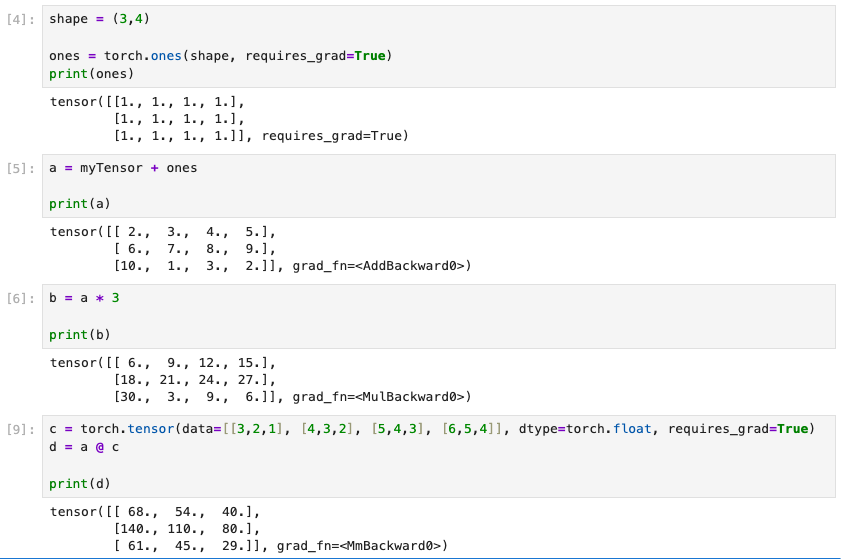
tensorcompu

可以看见a，b，c，d，这几个Tensor变量，都带有grad_fn的属性，它表示该Tensor是通过什么运算得到的。

Tensor的反向传播

Tensor的反向传播机制提供了一种可以跟踪计算的能力，但是只能针对于标量。

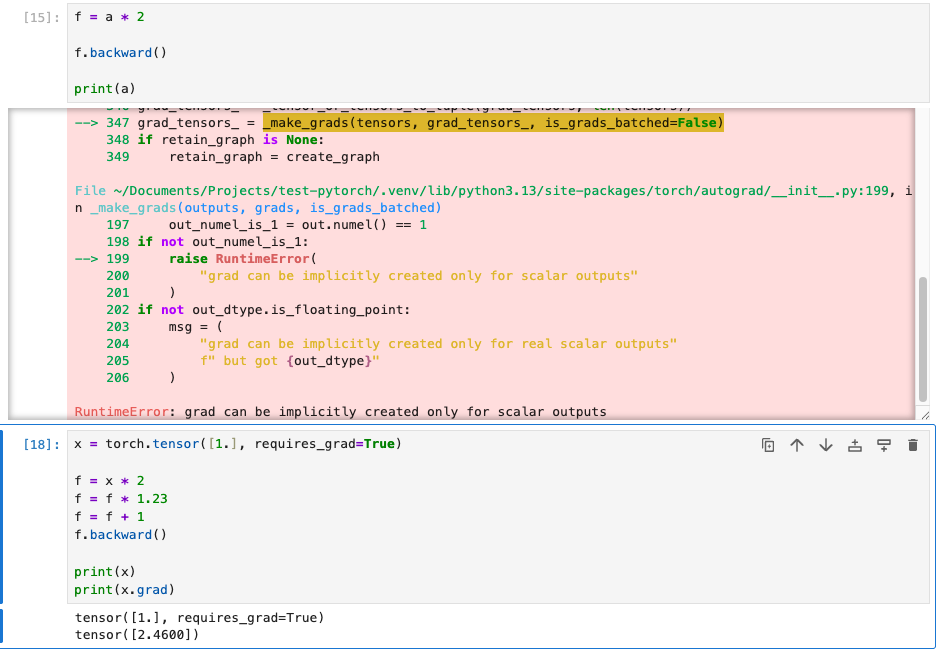
tensotgradscal

从上图可以看出，x标量被进行一系列的计算，最终都可以通过.grad的属性来得到梯度斜率。

Tensor除了介绍的以外，还有中位数，最大数，求和等等，详情可以参考官方资料。

三、使用 `torch.nn.Linear` 构建线性层

这里需要使用到torch中的Neural Network模块的线形模型，核心是构建一个基本的线形层：

python

linear_layer = torch.nn.Linear(in_features=1, out_features=1)

print(linear_layer.weight)
print(linear_layer.bias)

这一步等价于定义公式：

y = wx + b

其中：

weight 对应 $w$
bias 对应 $b$

四、定义线性回归模型

定义线形回归模型分为多个步骤。

第一步：准备好数据

这里的数据是用随机数生成公式中的X，然后通过基本计算加上一点随机数模拟噪音，以此模拟现实环境。

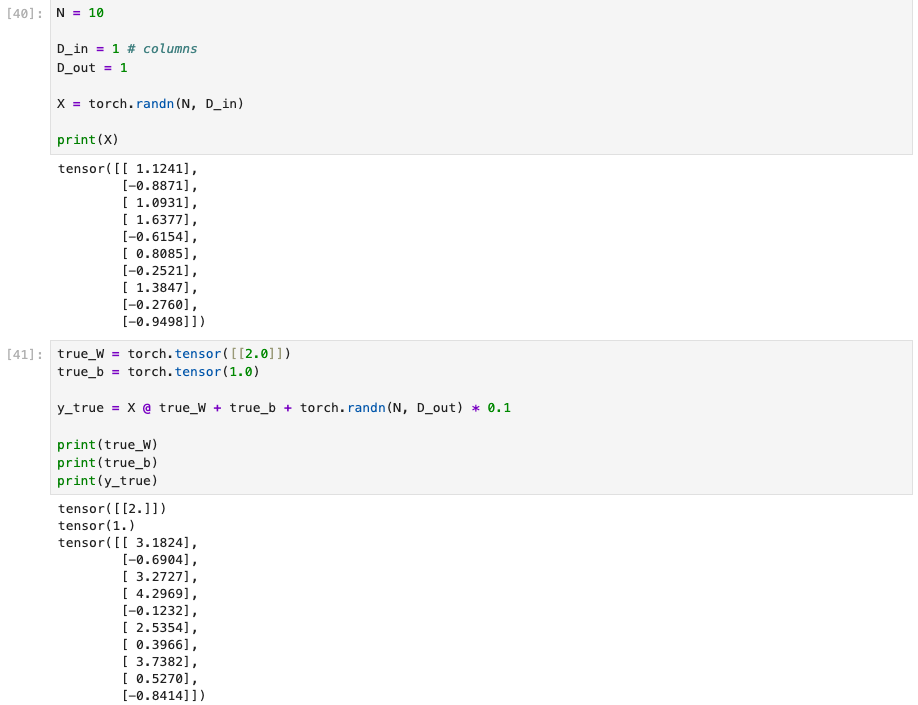
regrdata

其中，true_W和true_b是理论值，y_true是模拟结果值，我们通过数据模型训练找到接近理论值的W，'b'。

对应现实情况下，X可能是仪器的输入值（自变量），y_true是历史记录中的关于X对应的结果值（应变量），这段数据就是机器训练用的数据，现实情况中该数据量会很大。

第二步：定义回归模型

到这里了，实现的方法不是唯一的，虽然一般推荐使用继承torch.nn.Module的方式来定义模型，但是便于说明其内部原理，这里使用函数式，参数计算也是自己手动计算。

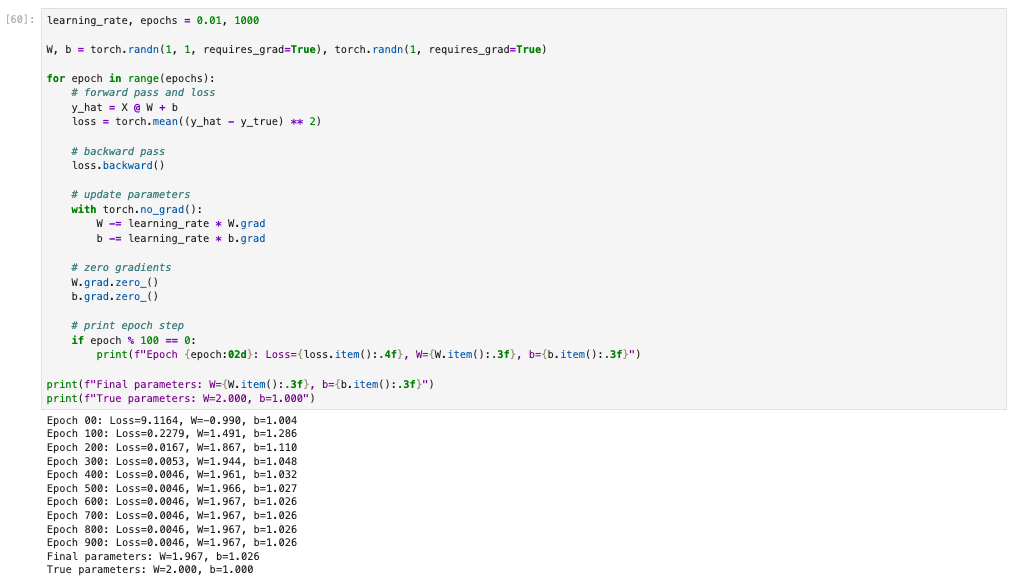
regrmodelfd

就是这么一个loop，我们就完成了模型训练。

五、Forward Pass（前向传播）

什么是前向传播

前向传播就是通过模型输入数据，进而得到预测结果。

输入数据 → 模型 → 得到预测结果

这里的模型是不准确的，得到的结果可能是错误的，需要进一步参数调整，才能提高准确度。

对应代码解释

下面是代码说明，具体代码：

python

# forward pass and loss
y_hat = X @ W + b

这里PyTorch自动构建计算图，并且记录计算关系（可以参考上面Tensor内容介绍）。

六、定义损失函数（Loss Function）

线性回归中最常用的是 均方误差（MSE）：

python

loss = torch.mean((y_hat - y_true) ** 2)

数学形式为：

\text{MSE} = \frac{1}{N} \sum (y - \hat{y})^2

损失值用于衡量模型预测的好坏，可见损失量越小越好。

七、Backward Pass（反向传播）

什么是反向传播

在前向传播时，构建了计算图，并且记录了计算关系。反向传播就是沿着计算图的相反方向传播，计算所有requires_grad=True的参数梯度。

对应代码解释

反向传播只有一行代码；

python

# backward pass
loss.backward()

通过这个反向函数调用，对于之前的两个参数：W，b。

我们可以将这两个参数的梯度斜率算出来。

八、参数更新

参数更新的核心代码片段：

python

# update parameters
with torch.no_grad():
    W -= learning_rate * W.grad
    b -= learning_rate * b.grad

# zero gradients
W.grad.zero_()
b.grad.zero_()

这里通过微调参数来减小上面的损失率，从而达到参数（W，b）接近理论值。

这里有两点注意：

为了使微调W，b时，不会把计算记录到计算图上，这里使用了torch.no_grad函数，在它作用下，计算Tensor不会记录到计算图上。
在完成参数更新后，我们需要重置W和b的梯度，避免累加到下次循环，从而产生混乱。

九、更高级的写法

对于实际场景下，一般模型训练不会像上面这样写，对于只有两个参数可以手动写写，但是一般LLM模型有7B，256B等等，这么多参数这样去写一点都不现实，对于手动计算那块代码，在torch中其实有现成的实现，除此之外它还有更多的内容，下面是展示一个更加通用的写法（使用继承torch.nn.Module的方式来定义模型，并且使用torch内部的实现机制）。

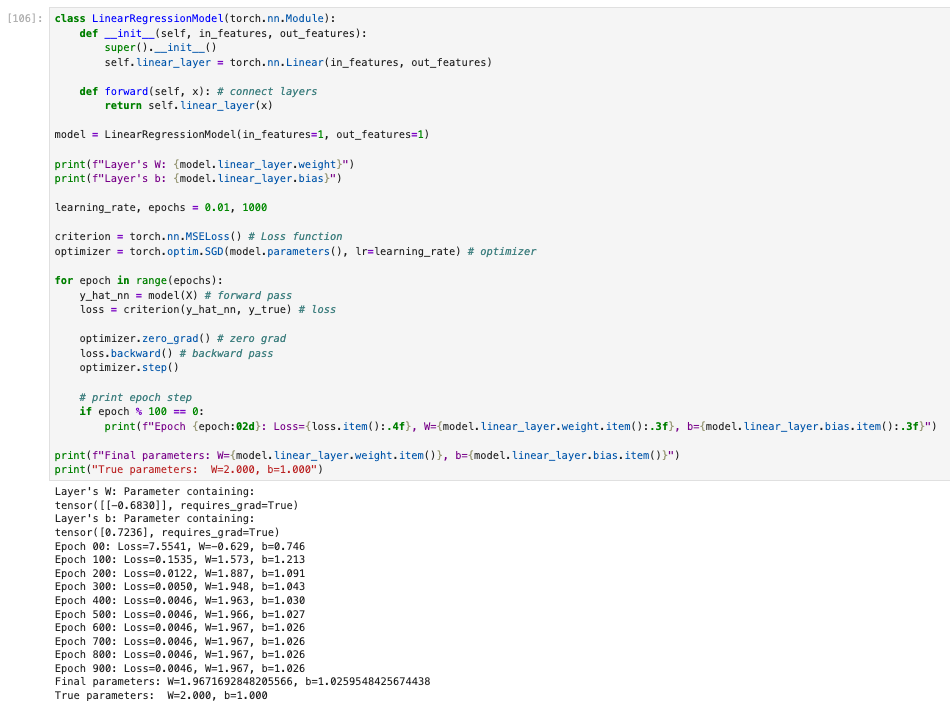
regrmodel

因为torch中对于常规的模型，优化器，损失函数都有定义，按照这种约定俗成的方式，对于参数更新那块全部被隐藏到了优化器中，处理非常优雅。

十、总结

通过本文的实战示例，我们从 最基础的数学模型 出发，完整走了一遍使用 PyTorch 训练线性回归模型的全过程，并逐步揭开了 PyTorch 自动求导与训练机制的“黑盒”。

核心收获可以归纳为以下几点：

线性回归的本质并不复杂 无论是数学公式
$y = wx + b$
还是 PyTorch 中的 nn.Linear，本质都是对这一公式的工程化封装。理解这一点，有助于你在学习更复杂模型时始终保持“模型直觉”。
Tensor 是 PyTorch 的核心数据结构 Tensor 不只是一个“多维数组”，当 requires_grad=True 时，它会成为计算图中的节点，自动参与梯度计算，这是 PyTorch 能够高效训练模型的基础。
Forward / Backward 构成了训练闭环
- Forward Pass：根据当前参数计算预测值与损失
- Backward Pass：根据损失反向计算梯度
- Parameter Update：利用梯度更新参数
这一流程不仅适用于线性回归，也适用于几乎所有深度学习模型。
理解“手写训练循环”非常重要 虽然在实际工程中我们通常会使用：
- nn.Module
- torch.optim
- nn.MSELoss
但通过手动实现参数更新与梯度清零，你可以真正理解：
- 梯度从哪里来
- 为什么要 zero_grad()
- 为什么参数更新要放在 torch.no_grad() 中
高级封装是建立在底层原理之上的 PyTorch 提供的高级 API 并不是“魔法”，而是对这些基础流程的高度抽象。当你理解了底层逻辑，再回过头看标准写法，会发现它既优雅又可靠。

总的来说，线性回归是学习 PyTorch 和深度学习的最佳起点。只要你真正理解了本文中的每一步，那么无论是多层神经网络、CNN、RNN，还是今天流行的大模型（LLM），它们在训练流程上都是一脉相承的。

后续你可以尝试的方向包括：

使用真实数据集（如房价、时间序列）
引入 Dataset / DataLoader
将模型迁移到 GPU（CUDA）
扩展到多维特征或多层网络

理解基础，才能走得更远。

← 返回所有文章列表

使用 PyTorch 进行线性回归模型训练实战 #

一、线性回归问题回顾 #

二、PyTorch 基础：Tensor 与自动求导 #

什么是Tensor #

Tensor的自动求导 #

Tensor的反向传播 #

三、使用 torch.nn.Linear 构建线性层 #

四、定义线性回归模型 #

第一步：准备好数据 #

第二步：定义回归模型 #

五、Forward Pass（前向传播） #

什么是前向传播 #

对应代码解释 #

六、定义损失函数（Loss Function） #

七、Backward Pass（反向传播） #

什么是反向传播 #

对应代码解释 #

八、参数更新 #

九、更高级的写法 #

十、总结 #

使用 PyTorch 进行线性回归模型训练实战

一、线性回归问题回顾

二、PyTorch 基础：Tensor 与自动求导

什么是Tensor

Tensor的自动求导

Tensor的反向传播

三、使用 `torch.nn.Linear` 构建线性层

四、定义线性回归模型

第一步：准备好数据

第二步：定义回归模型

五、Forward Pass（前向传播）

什么是前向传播

对应代码解释

六、定义损失函数（Loss Function）

七、Backward Pass（反向传播）

什么是反向传播

对应代码解释

八、参数更新

九、更高级的写法

十、总结