LZ77压缩算法

2018年4月1日

LZ77算法简介

LZ77算法是一种无损压缩算法，最早由两位以色列人于1977发表，它是一种典型的字典型压缩算法，目前几乎大多数的无损压缩算法都是基于这个LZ77算法，也就是在其基础上优化修改，此算法可以称得上是无损压缩算法界的鼻祖了。

参考维基百科lz77

算法逻辑

LZ77的算法核心就是一个滑动窗口，在滑动窗口里面搜索重复字节，并将匹配到的字节串用更短的字节串方式表示出来。

这里涉及到几个要素：

滑动窗口缓冲区
滑窗的前部区域
滑窗的已编码区域

编码流程

编码步骤：

首先分配一块缓冲区域用来处理数据
初始的前部区域为空
初始的已编码区域也为空
加载的字节流到前部区域，是否最后一个字节，是则进行第8步，否则继续第5步
在已编码区域寻找匹配字节串，如果找到进行第6步，否则进行第7步
将匹配到的第一个字节的相对位置和长度，标记到已编码区域中，继续第4步
将前部区域的字节直接拷贝到已编码区域，继续第4步
编码结束

编码图示：

当滑动窗口还没有处理数据时：

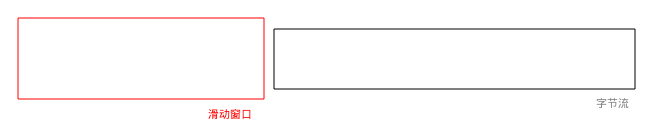
stepprecomp

当滑动窗口开始处理数据时：

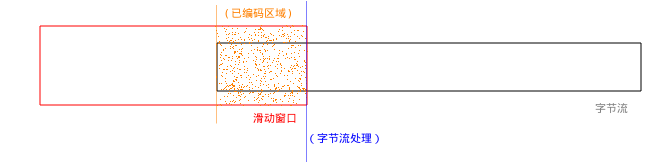
stepcomp

当滑动窗口正在处理数据时：

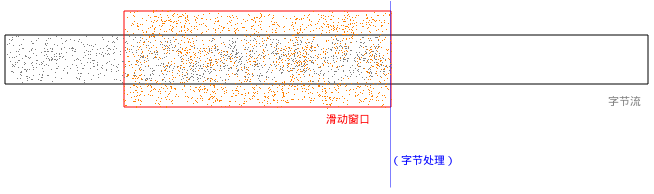
stepcomping

当数据快要处理完时：

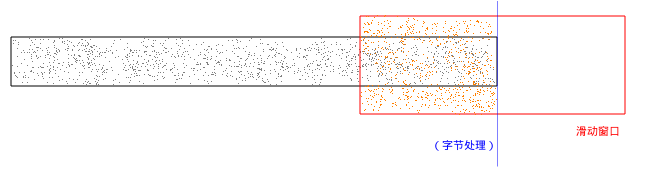
stepcompfin

整个过程如同字节流在这个滑动窗口的黑盒子里面流动过一样，然后，它被加工的数据是已经压缩的数据了。

数据编码中，会涉及到如何标记数据，在lz77算法中是用2-3个字节来表示的，即：如果有两个自己是'\0'，则表示它是一个直译字节，是直接拷贝过来的字节，这两个'\0'后面的字节就是原始字节；否则，这两个字节是表示当前字节处应该填充的字节串应该在的相对位置和长度（你甚至可以为你自己的lz77编码器自定义数据标记方式）。

解码流程

解码的过程是编码过程的逆过程。

解码步骤：

字节流是否是最后字节，是则进行第5步，否则进行第2步
从字节流获取两个字节，如果是\0x00\0x00则进行第3步，否则进行第4步
将\0x00\0x00后面的一个字节复制到输出缓存区域，继续加载字节流，继续第1步
从两个字节的编码中得到在滑动窗口的相对偏移和内容长度，把偏移处的内容拷贝到当前输出缓存，继续第1步
解码结束

上面的输出缓存区域是指在字节处理位置处理过后的字节流存放的缓存区域就是输出缓存

解码图示：

滑动窗口还没有输入数据的时候：

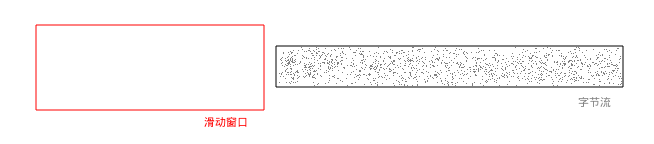
stepuncomp

滑动窗口开始处理数据的时候：

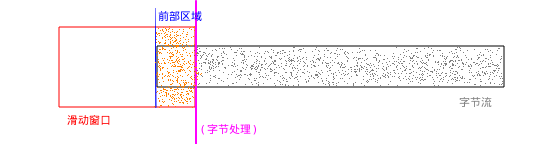
stepuncomp

数据在滑动窗口中处理：

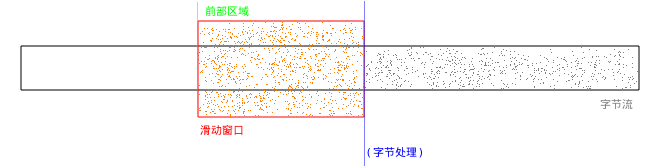
stepuncomping

数据快要处理完的时候：

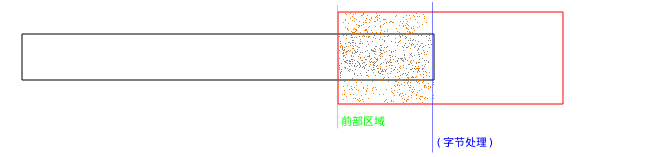
stepuncompfin

源码实现

辅助函数：

unsigned int search_maxlen_p( unsigned char**  pt, \
                              unsigned char* head, \
                              unsigned char* tail, \
                              unsigned char* end)
{
  unsigned char* tmp = *pt;
  unsigned int leng = 0, i;

  for(tmp;tmp >= head;tmp--){
    if(tmp[0] == tail[0]){
      for(i = 0;(i < ((1 << LENGTHBITS) - 1)) && (&tmp[i] > head) && (&tmp[i] < tail) && (&tail[i] < end) && (tmp[i] == tail[i]);i++);
      if(i > leng){
        leng = i;
        *pt = tmp;
      }
    }
  }
  return leng;
}

编码实现：

int lz77_encode(FILE* in,FILE* out)
{
  unsigned char* buf = 0,* head = 0,* tail = 0;
  long size = 0;

  if(! in || ! out)return 1;

  get_filesize(in,size); // get file size.
  if(size <= 0)return 1;

  buf = (unsigned char*)malloc(size* sizeof(unsigned char)); // allocate memory.
  if(! buf)return 1;

  if(fread(buf,sizeof(unsigned char),size,in) == size){
    head = tail = buf;
    fputc((size >> 24) & 0xff,out);
    fputc((size >> 16) & 0xff,out);
    fputc((size >>  8) & 0xff,out);
    fputc((size >>  0) & 0xff,out);

    for(;;){ // loop block.
      head = tail - WINDOWSIZE;
      if(buf  > head)head = buf;
      if(tail > buf + size - 1)break;
      if(tail > head){
        unsigned char* pt = tail - 1;
        unsigned int bytes = 0;
        bytes = search_maxlen_p(&pt,head,tail,buf + size);
        // search maximal matched bytes and position.
        if(bytes > 0){
          unsigned char chars[2] = {0};
          chars[0] = (unsigned char)(( (tail - pt) >> LENGTHBITS) & 0xff);
          chars[1] = (unsigned char)((((tail - pt) << LENGTHBITS) + bytes) & 0xff);
          fputc(chars[0],out);
          fputc(chars[1],out);
          //fprintf(stderr,"{%d - %d}",tail - pt,bytes);
          tail += bytes;
        } else {
          fputc(0,out);
          fputc(0,out);
          fputc(*tail,out);
          tail++;
        }
      } else {
        fputc(0,out);
        fputc(0,out);
        fputc(*tail,out);
        tail++;
      }
    }

  }

  free(buf);
  return 0;
}

解码实现：

int lz77_decode(FILE* in,FILE* out)
{
  unsigned char* nbuf = 0,* ori_buf = 0,* head = 0,* tail = 0;
  long ori_size = 0,nsize = 0;

  if(! in || ! out)return 1;

  get_filesize(in,nsize); // get file size.
  if(nsize <= 0)return 1;

  ori_size  = (fgetc(in) & 0xff) << 24;
  ori_size += (fgetc(in) & 0xff) << 16;
  ori_size += (fgetc(in) & 0xff) <<  8;
  ori_size += (fgetc(in) & 0xff) <<  0;
  if(ori_size <= 0)return 1;

  nbuf = (unsigned char*)malloc(nsize* sizeof(unsigned char));
  if(! nbuf)return 1;

  ori_buf = (unsigned char*)malloc(ori_size* sizeof(unsigned char));
  if(ori_buf){
    head = tail = ori_buf; // store head and tail of slide-window.

    if(fread(nbuf,sizeof(unsigned char),nsize,in) == (nsize - 4)){
      unsigned char* pt  = nbuf;

      for(;;){
        if(pt >= (nbuf + nsize - 4))break;
        if(! pt[0] && ! pt[1] ){ // \0\0\?
          tail[0] = pt[2];
          tail++;
          pt += 3;
        } else { // \?\?
          unsigned int offset = 0,length = 0,i;
          offset  =  pt[0] << LENGTHBITS;
          offset += (pt[1] >> LENGTHBITS) & 0x0f;
          length  =  pt[1] & 0x0f;
          //fprintf(stderr,"{%d - %d}",offset,length);
          for(i = 0;i < length;i++){
            tail[i] = ((unsigned char*)(tail - offset))[i];
          }
          tail += length;
          pt += 2;
        }
      }
      fwrite(ori_buf,sizeof(unsigned char),ori_size,out);
    }

    free(ori_buf);
  }

  free(nbuf);
  return 0;
}